El “CURSO DE MATEMÁTICAS DISCRETAS” es un blog creado con el fin de ayudar aquellas personas que necesiten información o guía para entender de manera clara y sencilla las matemáticas discretas pueda encontrar eso que buscan en este blog.
Los conceptos matemáticos que se desean transmitir a las personas por medio de este blog son:
- Los sistemas numéricos: que los componen los números binarios, decimales, octales, hexadecimales, entre otros.
-Conversión entre sistemas numéricos
-Complementos
-Lógica combinacional (Circuitos, Álgebra de Boole, entre otros).
¿QUE SON LAS MATEMÁTICAS DISCRETAS?
Las matemáticas discretas son un área de las matemáticas encargadas del estudio de los conjuntos discretos: finitos o infinitos numerables.
La matemáticas discretas estudian estructuras cuyos elementos pueden contarse uno por uno separadamente. Es decir, los procesos en matemáticas discretas son contables, como por ejemplo, los números enteros, grafos y sentencias de lógica.
La matemáticas discretas estudian estructuras cuyos elementos pueden contarse uno por uno separadamente. Es decir, los procesos en matemáticas discretas son contables, como por ejemplo, los números enteros, grafos y sentencias de lógica.
uno de los usos de las matemáticas discretas es...
La teoría de la informática incluye áreas de la matemática discreta relevante a la computación. Está altamente relacionada con teoría de grafos y lógica. Dentro de la teoría de la informática se encuentra la teoría de algoritmos para problemas matemáticos. La computabilidad estudia lo que puede ser computado y tiene lazos fuertes con la lógica, mientras que la complejidad estudia el tiempo que se demora en hacer computaciones. La teoría de autómatas y los lenguajes formales se relacionan de manera cercana con la computabilidad. Las redes de Petri y álgebra de procesos se usan para modelar sistemas computacionales, y métodos de la matemática discreta se usan para analizar circuitos VLSI. La geometría computacional aplica algoritmos a problemas geométricos, mientras que el análisis digital de imágenes los aplica a representaciones de imágenes. La teoría informática también incluye el estudio de tópicos de informática continua.
SISTEMAS NUMERICOS
Un sistema de numeración es un conjunto de símbolos y reglas de generación que permiten construir todos los números válidos.Un sistema de numeración puede representarse como
N=(S,R)
donde:
N es el sistema de numeración considerado (por ej. decimal, binario, etc.).
S es el conjunto de símbolos permitidos en el sistema. En el caso del sistema decimal son {0,1,...9}; en el binario son {0,1}; en el octal son {0,1,...7}; en el hexadecimal son {0,1,...9,A,B,C,D,E,F}.
R son las reglas que nos indican qué números son válidos en el sistema, y cuáles no. En un sistema de numeración posicional las reglas son bastante simples, mientras que la numeración romana requiere reglas algo más elaboradas.
Estas reglas son diferentes para cada sistema de numeración considerado, pero una regla común a todos es que para construir números válidos en un sistema de numeración determinado sólo se pueden utilizar los símbolos permitidos en ese sistema.
Para indicar en qué sistema de numeración se representa una cantidad se añade como subíndice a la derecha el número de símbolos que se pueden representar en dicho sistema.
N=(S,R)
donde:
N es el sistema de numeración considerado (por ej. decimal, binario, etc.).
S es el conjunto de símbolos permitidos en el sistema. En el caso del sistema decimal son {0,1,...9}; en el binario son {0,1}; en el octal son {0,1,...7}; en el hexadecimal son {0,1,...9,A,B,C,D,E,F}.
R son las reglas que nos indican qué números son válidos en el sistema, y cuáles no. En un sistema de numeración posicional las reglas son bastante simples, mientras que la numeración romana requiere reglas algo más elaboradas.
Estas reglas son diferentes para cada sistema de numeración considerado, pero una regla común a todos es que para construir números válidos en un sistema de numeración determinado sólo se pueden utilizar los símbolos permitidos en ese sistema.
Para indicar en qué sistema de numeración se representa una cantidad se añade como subíndice a la derecha el número de símbolos que se pueden representar en dicho sistema.
Sistema Binario
El sistema de numeración binario solo tiene dos dígitos. El sistema binario con sus dos dígitos es un sistema en base dos. Los dígitos binarios (bits) son 0 y 1.
• La posición de un 1 o de un 0 en un número binario indica su peso, o valor dentro del número, así como la posición de un dígito decimal determina el valor de ese dígito.
• Los pesos de un número binario están basados en las potencias de dos.
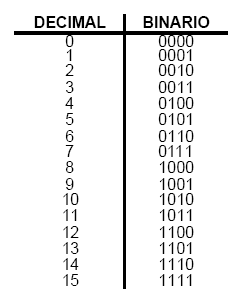
Contar en Binario
Por ejemplo, se requieren cuatro bits para contar desde 0 hasta 15. En general, con n bits se puede contar hasta un número igual a 2n-1. Máximo número decimal = 2n-1
Así, con 5 bits (n = 5) se puede contar desde 0 hasta 31: 25 – 1 = 32 – 1 = 31
Con 6 bits (n = 6) se puede contar desde 0 hasta 63: 26 - 1 = 64 – 1 = 63
sistema decimal
El sistema numérico decimal que
utilizamos para representarlos números, utiliza diez símbolos llamados cifras.
Este sistema de numeración es el más usado, tiene como base el número 10, ósea
que posee 10 dígitos (o símbolos) diferentes (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). El
sistema de numeración decimal fue desarrollado por los hindúes, posteriormente
lo introducen los árabes en Europa, donde recibe el nombre de sistema de
numeración decimal o arábigo.
sistema octal
El sistema numérico en base 8 se llama
octal y utiliza los dígitos 0 a 7. El sistema de numeración es una base que es
potencia exacta de 2 o de la numeración binaria. Hace que la conversión a binario o viceversa
sea bastante simple. El sistema octal usa 8 dígitos (0, 1, 2, 3, 4, 5, 6,7) y
tienen el mismo valor que en el sistema de numeración decimal.
sistema hexadecimal
El sistema numérico en base 16 se llama
Hexadecimal y utiliza los dígitos 0 a F. El sistema de numeración es una base
que es potencia exacta de 2 o de la numeración binaria. Esta característica
hace que la conversión a binario o viceversa sea bastante simple. El sistema
Hexadecimal usa 16 dígitos (0, 1, 2, 3, 4, 5,6, 7, 8, 9, A, B, C, D, E, F) y
tienen el mismo valor que en el sistema de numeración decimal hasta el 9, las
letras tienen el valor de A=10, B=11, C=12, D=13, E=14, F=15.
Hexadecimal
|
Decimal
|
Hexadecimal
|
Decimal
|
0
|
0
|
8
|
8
|
1
|
1
|
9
|
9
|
2
|
2
|
A
|
10
|
3
|
3
|
B
|
11
|
4
|
4
|
C
|
12
|
5
|
5
|
D
|
13
|
6
|
6
|
E
|
14
|
7
|
7
|
F
|
15
|
Conversiones
CONVERSIÓN DE UN NUMERO
DECIMAL A BINARIO
Para esta transformación
es necesario tener en cuenta los pasos que mostraremos en el siguiente ejemplo:
Transformemos el numero 42 a numero binario
1. Dividimos el número 42 entre 2
2. Dividimos el cociente obtenido por 2 y repetimos el mismo procedimiento hasta que el cociente sea 1.
3. El numero binario lo formamos tomando el primer dígito de derecha a izquierda, como se muestra en el siguiente esquema.
El ultimo cociente, seguidos por los residuos obtenidos en cada división, seleccionándolos
1. Dividimos el número 42 entre 2
2. Dividimos el cociente obtenido por 2 y repetimos el mismo procedimiento hasta que el cociente sea 1.
3. El numero binario lo formamos tomando el primer dígito de derecha a izquierda, como se muestra en el siguiente esquema.
El ultimo cociente, seguidos por los residuos obtenidos en cada división, seleccionándolos
CONVERSIÓN DE UN NUMERO
DECIMAL FRACCIONARIO A UN NÚMERO BINARIO
Para transformar un
número decimal fraccionario a un número binario debemos seguir los pasos que
mostramos en el siguiente ejemplo: transformemos el número 42,375.
1. la parte entera se transforma de igual forma que el ejemplo anterior.
2. La parte fraccionaria de la siguiente manera:
Multiplicamos por el numero 2 y tomamos la parte entera del producto que ira formando el numero binario correspondiente
Tomamos nuevamente la parte entera del producto, y la parte fraccionaria la multiplicamos sucesivamente por 2 hasta llegar a 0
Tomamos nuevamente la parte entera, y como la parte fraccionaria es 0, indica que se ha terminado el proceso. El numero binario correspondiente a la parte decimal será la unión de todas las partes enteras, tomadas de las multiplicaciones sucesivas realizadas durante el transcurso del proceso , en donde el primer dígito binario corresponde a la primera parte entera , el segundo dígito a la segunda parte entera , y así sucesivamente hasta llegar al último .Luego tomamos el numero binario , correspondiente a la parte entera , y el numero binario , correspondiente a la parte fraccionaria y lo unimos en un solo número binario correspondiente a el numero decimal.
1. la parte entera se transforma de igual forma que el ejemplo anterior.
2. La parte fraccionaria de la siguiente manera:
Multiplicamos por el numero 2 y tomamos la parte entera del producto que ira formando el numero binario correspondiente
Tomamos nuevamente la parte entera del producto, y la parte fraccionaria la multiplicamos sucesivamente por 2 hasta llegar a 0
Tomamos nuevamente la parte entera, y como la parte fraccionaria es 0, indica que se ha terminado el proceso. El numero binario correspondiente a la parte decimal será la unión de todas las partes enteras, tomadas de las multiplicaciones sucesivas realizadas durante el transcurso del proceso , en donde el primer dígito binario corresponde a la primera parte entera , el segundo dígito a la segunda parte entera , y así sucesivamente hasta llegar al último .Luego tomamos el numero binario , correspondiente a la parte entera , y el numero binario , correspondiente a la parte fraccionaria y lo unimos en un solo número binario correspondiente a el numero decimal.
CONVERSIÓN DE UN NÚMERO BINARIO A UN NUMERO DECIMAL
Para convertir un número binario a decimal,
realizamos los siguientes pasos:
1. Tomamos los valores de posición correspondiente a las columnas donde aparezcan únicamente unos
2. Sumamos los valores de posición para identificar el número decimal equivalente
1. Tomamos los valores de posición correspondiente a las columnas donde aparezcan únicamente unos
2. Sumamos los valores de posición para identificar el número decimal equivalente
CONVERSIÓN DE UN NUMERO DECIMAL A OCTAL
Para convertir un número en el sistema decimal al
sistema de numeración Octal, debemos seguir los pasos que mostraremos en el
siguiente ejemplo Convertir el número decimal 323.625 a el sistema de
numeración Octal
1. Se toma el numero entero y se divide entre 8 repetidamente hasta que el dividendo sea menor que el divisor, para colocar entonces el número 0 y pasar el dividendo a formar el primer dígito del número equivalente en decimal
2. Se toma la parte fraccionaria del número decimal y la multiplicamos por 8 sucesivamente hasta que el producto no tenga números fraccionarios
3. Pasamos la parte entera del producto a formar el dígito correspondiente
4. Al igual que los demás sistemas, el número equivalente en el sistema decimal, está formado por la unión del número entero equivalente y el número fraccionario equivalente.
1. Se toma el numero entero y se divide entre 8 repetidamente hasta que el dividendo sea menor que el divisor, para colocar entonces el número 0 y pasar el dividendo a formar el primer dígito del número equivalente en decimal
2. Se toma la parte fraccionaria del número decimal y la multiplicamos por 8 sucesivamente hasta que el producto no tenga números fraccionarios
3. Pasamos la parte entera del producto a formar el dígito correspondiente
4. Al igual que los demás sistemas, el número equivalente en el sistema decimal, está formado por la unión del número entero equivalente y el número fraccionario equivalente.
CONVERSIÓN DE UN NUMERO OCTAL A BINARIO
La ventaja principal del sistema de numeración
Octal es la facilidad con que pueden realizarse la conversión entre un número
binario y octal. A continuación mostraremos un ejercicio que ilustrará la
teoría. Por medio de este tipo de conversiones, cualquier número Octal se
convierte a binario de manera individual. En este ejemplo, mostramos claramente
el equivalente 100 111 010 en binario de cada número octal de forma individual.
CONVERSIÓN DE UN NUMERO
DECIMAL A UN NUMERO HEXADECIMAL
Convertir el número 250.25 a Hexadecimal
1. Se toma la parte entera y se divide sucesivamente por el numero decimal 16 (base) hasta que el cociente sea 0
2. Los números enteros resultantes de los cocientes, pasarán a conformar el número hexadecimal correspondiente, teniendo en cuenta que el sistema de numeración hexadecimal posee solo 16 símbolos, donde los números del 10 hasta el 15 tienen símbolos alfabéticos que ya hemos explicado
3. La parte fraccionaria del número a convertir se multiplica por 16 (Base) sucesivamente hasta que el producto resultante no tenga parte fraccionaria
4. Al igual que en los sistemas anteriores, el número equivalente se forma, de la unión de los dos números equivalentes, tanto entero como fraccionario, separados por un punto que establece la diferencia entre ellos.
CONVERSIÓN DE UN NUMERO
HEXADECIMAL A UN NUMERO DECIMAL
Como en los ejemplos
anteriores este también nos ayudará a entender mejor este procedimiento:
Convertir el numero hexadecimal 2B6 a su equivalente decimal.
1. Multiplicamos el valor de posición de cada columna por el dígito hexadecimal correspondiente.
2. El resultado del número decimal equivalente se obtiene, sumando todos los productos obtenidos en el paso anterior.
1. Multiplicamos el valor de posición de cada columna por el dígito hexadecimal correspondiente.
2. El resultado del número decimal equivalente se obtiene, sumando todos los productos obtenidos en el paso anterior.
complementos
Los complementos se utilizan para simplificar la operación de resta y efectuar manipulaciones lógicas.
Hay dos tipos de complementos para cada sistema de base r: el complemento a la base (complemento a r) y el complemento a la base disminuida (complemento a r-1).
Si sustituimos el valor de la base r en estos nombres, los dos tipos son el complemento a dos y el complemento a uno, en el caso de los números binarios, y el comportamiento a diez y el complemento a nueve en el caso de los números decimales.
Complemento a la base disminuida
Dado un número N en base a r que tiene n dígitos, el complemento a (r - 1) de N se define como (rn - 1) - N. En el caso de números decimales, r = 10 y r - 1 =9, así que el complemento a nueve de N es (10n - 1) - N. En este caso, 10 n representa un número que consiste en un uno seguido de ceros. 10n - 1 es un número representado pos n nueves.
Por Ejemplo, si n = 4, tenemos 104 = 10,000 y 104 - 1 =9999
De esto se sigue que el complemento a nueve de un número decimal se obtiene restando cada digito nueve.
En caso de LOS NÚMERO BINARIOS r = 2 y r - 1 = 1, así que el complemento a uno de N es (2n -1) - N. Aquí también, 2n se representa con un número binario que consiste en un uno seguido de n ceros. 2n -1 es un número binario representado por n unos.
Por Ejemplo, si n = 4, tenemos 24 = (10000)2 y 24 - 1 = (1111)2
El complemento a uno de un número binario se obtiene restando cada digito a uno. Por lo tanto el complemento a uno de un número binario se forma cambiando los unos a ceros y los ceros a unos.
Por Ejemplo
El complemento a uno de 1011000 es 0100111
El complemento a uno de 0101101 es 1010010
El complemento a (r - 1) de los números octales y hexadecimales se obtiene restando cada dígito a 7 y F (15 decimal), respectivamente.
Complemento a la Base
El complemento a r de un número N de n dígitos en base a r se define como rn - N, para N no igual a 0, y 0 para N = 0. Si comparamos con el complemento a (r - 1), veremos que el complemento a r se obtiene sumando 1 al componente a (r - 1), ya que rn - N = [(rn - 1) -N] + 1. Así pues, el complemento a 10 del complemento del número decimal 2389 es 7610 + 1 = 7611, y se obtiene sumando 1 al valor del complemento a nueve. El complemento a dos del número binario 101100 es 010011 + 1 = 010100, y se obtiene sumando 1 al valor del complemento a uno.
Puesto que 10n es un número que se representa con un uno seguido de n ceros, 10n - N, que es el complemento a 10 de N, también puede formarse dejando como están todos los ceros menos significativos, restando a 10 el primer dígito menos significativo distinto de cero, y restando a 9 los demás dígitos a la izquierda.
El complemento a 10 de 012398 es 987602
El complemento a 10 de 246700 es 753300
El complemento a 10 del primer número que se representa con un uno seguido de n ceros, 10n - N, que significa y restando a 9 todos los demás dígitos. El complemento a 10 del segundo número se obtiene dejando como están los dos ceros de la derecha, restando 7 a 10 y restando 9 los otros tres dígitos.
De forma similar, el complemento a dos se forma dejando como están todos los ceros menos significativos y el primer uno, y sustituyendo los unos por ceros y los ceros por unos en las demás posiciones a la izquierda.
El complemento a dos de 1101100 es 0010100
El complemento a dos de 0110111 es 1001001
El complemento a dos del primer número se obtiene dejando como están los dos ceros menos significativos y el primer uno, y sustituyendo después los unos por ceros y los ceros por unos en las cuatro posiciones más significativas. El complemento a dos del segundo número se obtiene dejando como está el uno menos significativo y complementando todos los demás dígitos a la izquierda.
Si el número N original lleva punto, deberá quitarse temporalmente para formar el complemento a r o a (r - 1), y volver a colocarlo después en el número completando en la misma posición relativa.
El complemento a r de N es rn - N. El complemento del complemento es rn - (rn - N) = N, o sea, el número original.
Lógica combinacional
Se denomina sistema combinacional o lógica combinacional a todo sistema digital en el que sus salidas son función exclusiva del valor de sus entradas en un momento dado, sin que intervengan en ningún caso estados anteriores de las entradas o de las salidas. Las funciones (OR, AND, NAND, XOR) son booleanas (de Boole) donde cada función se puede representar en una tabla de la verdad. Por tanto, carecen de memoria y de retroalimentación.
Estos circuitos están compuestos únicamente por puertas lógicas interconectadas entre sí.

Funciones combinacionales
Todos los circuitos combinacionales pueden representarse empleando álgebra de Boole a partir de su función lógica, generando de forma matemática el funcionamiento del sistema combinacional. De este modo, cada señal de entrada es una variable de la ecuación lógica de salida. Por ejemplo, un sistema combinacional compuesto exclusivamente por una puerta AND tendría dos entradas A y B. Su función combinacional seria![]() , para una puerta OR sería
, para una puerta OR sería![]() . Estas operaciones se pueden combinar formando funciones más complejas.
. Estas operaciones se pueden combinar formando funciones más complejas.
Esto permite emplear diferentes métodos de simplificación para reducir el número de elementos combinacionales que forman el sistema.
Circuitos
Un circuito lógico es aquél que maneja la información en forma binaria, es decir, con valores de "1" y "0".
Estos dos niveles lógicos de voltaje fijos representan:
· "1" nivel alto o "high".
· "0" nivel bajo o "low".
Todos los circuitos cuyos componentes realizan operaciones análogas a las que indican los operadores lógicos se llaman "Circuitos Lógicos" o "circuitos digitales".
Los Circuitos Lógicos están compuestos por elementos digitales como la compuerta AND (Y), compuerta OR (O), compuerta NOT (NO) y otras combinaciones muy complejas de los circuitos antes mencionados.
Estas combinaciones (ya mencionadas) dan lugar a otros tipos de elementos digitales. Aquí hay un listado de algunos de éstos.: compuerta NAND (No Y); compuerta NOR (No O); compuerta OR exclusiva (O exclusiva)

Estos circuitos están compuestos únicamente por puertas lógicas interconectadas entre sí.

Funciones combinacionales
Todos los circuitos combinacionales pueden representarse empleando álgebra de Boole a partir de su función lógica, generando de forma matemática el funcionamiento del sistema combinacional. De este modo, cada señal de entrada es una variable de la ecuación lógica de salida. Por ejemplo, un sistema combinacional compuesto exclusivamente por una puerta AND tendría dos entradas A y B. Su función combinacional seria
Esto permite emplear diferentes métodos de simplificación para reducir el número de elementos combinacionales que forman el sistema.
Circuitos
Un circuito lógico es aquél que maneja la información en forma binaria, es decir, con valores de "1" y "0".
Estos dos niveles lógicos de voltaje fijos representan:
· "1" nivel alto o "high".
· "0" nivel bajo o "low".
Todos los circuitos cuyos componentes realizan operaciones análogas a las que indican los operadores lógicos se llaman "Circuitos Lógicos" o "circuitos digitales".
Los Circuitos Lógicos están compuestos por elementos digitales como la compuerta AND (Y), compuerta OR (O), compuerta NOT (NO) y otras combinaciones muy complejas de los circuitos antes mencionados.
Estas combinaciones (ya mencionadas) dan lugar a otros tipos de elementos digitales. Aquí hay un listado de algunos de éstos.: compuerta NAND (No Y); compuerta NOR (No O); compuerta OR exclusiva (O exclusiva)

leyes del algebra de Boole y ley de morgan
Leyes
Básicas del Álgebra de Boole
• Leyes
básicas del Álgebra de Boole:
– Leyes
conmutativas de la suma y multiplicación.
– Leyes
asociativas de la suma y multiplicación.
– Ley
distributiva.
• Son
las mismas que las del álgebra ordinaria.
Leyes
Conmutativas
• El
orden en que se aplica a las variables la operación OR es indiferente:
A+B
= B+A
• El
orden en que se aplica a las variables la operación AND es indiferente:
AB
= BA
Ley
conmutativa de la suma para dos variables
Ley
conmutativa de la multiplicación para dos variables
Leyes
Asociativas
• Al
aplicar la operación OR a más de dos variables, el resultado es el mismo
independientemente de la forma en que se agrupen las variables:
A
+ (B + C) = (A + B) + C
• Al
aplicar la operación AND a más de dos variables, el resultado es el mismo
independientemente de la forma en que se agrupen las variables:
A (BC)
= (AB) C
Ley
asociativa de la suma para tres variables
Ley
asociativa de la multiplicación para tres variables
Ley
Distributiva
• Aplicar
la operación OR a dos o más variables y luego aplicar la operación AND al
resultado de la operación y a otra variable aislada, es equivalente a aplicar
la operación AND a la variable aislada con cada uno de los sumandos y luego
aplicar la operación OR a los productos resultantes.
• Esta
ley también expresa el proceso de sacar factor común, en el que la variable
común se saca como factor de los productos parciales.
A(B
+ C) = AB + AC
Ley
distributiva para tres variables
Reglas Básicas del Álgebra de Boole
Muy
útiles para la manipulación y simplificación de expresiones booleanas.
1. A
+ 0 = A
2. A
+ 1 = 1
3. A
·0 = 0
4. A
·1 = A
5. A
+ A = A
6. A
+ A = 1
7. A
·A = A
8. A
·A = 0
9. A
= A
10. A
+ AB = A
11. A
+ AB = A + B
12. (A
+ B)(A + C) = A + BC
A,
B, o C pueden representar una única variable o una combinación de variables.
Leyes de
Morgan
Para
todo par de variables lógicas a, b 0 A, se cumple...
a + b = a*b y a*b =a + b
Para
demostrar esto: a + b = a*b
Si
demostramos que siempre se cumple (a + b) + (a*b) = 1 y (a +b) *(a*b) = 0, es
porque (a + b) y (a*b) son siempre
opuestos, o sea, porque (a +b) y(a*b) son siempre iguales.
(a+ b) * (a *b) = [(a + b)+a]
* [(a + b)+b] = (1+b) * (1+a) = 1*1 = 1(a + b) * (a*b) = [a*(a*b)] + [b*(a*b)]
= (0*b) + (0*a) = 0+0 = 0
Estas
dos leyes son muy importantes, ya que permiten pasar de expresiones en sumas
lógicas a expresiones equivalentes en productos lógicos.
Suscribirse a:
Comentarios (Atom)








